寺社建築や町屋風建物等の振動特性を伝統耐震診断を用いて調べてみると、在来型の建物の振動特性とはかなり相違することが分かりました。
下図『伝統構法の建物の固有周期の比較』は伝統工法による建物(traditional buildings)の実測された固有周期の例です。
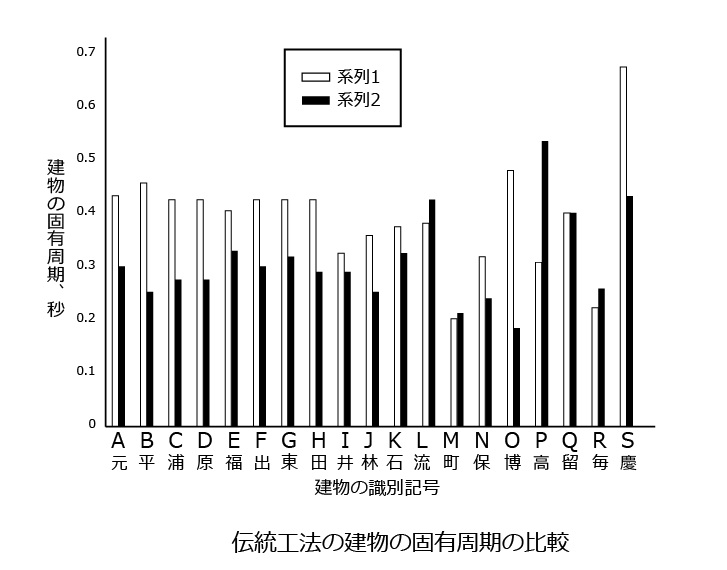
これを見ると下図の在来型の建物の固有周期に比べて、伝統工法による建物の固有周期が全体的にかなり大きいことが分かります。
これは在来型の建物が構造要素の壁を多く設けて強度を確保している言わば「剛構造」の建物と分類するならば、伝統工法による建物は構造要素の壁が殆ど設けられていない「柔構造」の建物であることの表れです。
したがって伝統工法の建物の伝統耐震診断を、在来工法の建物と同様な考えで行う場合には、建物の基準固有周期Ttは、上記『伝統工法の建物の固有周期の比較』の図から分かるように 0.2 秒とするのが適当であると考えられます。
また伝統工法による建物は横方向からの力に対する抵抗力が小さく、大きく変形しやすいので、最大応答倍率も、在来型の建物のそれに比べると非常に大きいのです。
伝統耐震診断による性能評価
伝統工法の建物は構造要素壁が一般に殆どない為、水平方向に変形しやすく、大きな変位の振幅で振動する場合でも、在来型の建物に比べても破壊しにくい、しなやかな性質の構造物になっていると考えられます。
下図は日本建築学会と京都大学防災研究所が示している、在来型の建物と伝統的建物の変形特性の違いを比較したものです。
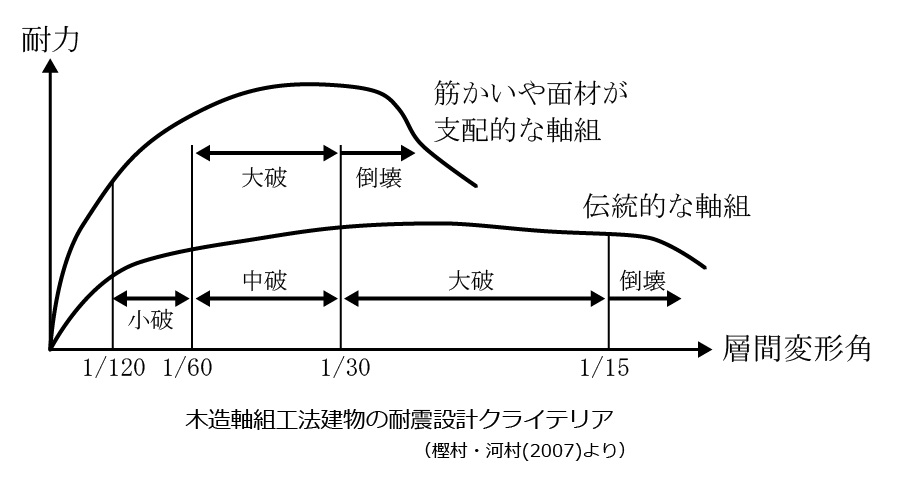
これを見ると在来型の建物が1/30 radianの層間変形角(約2度)が破壊の目安になっているに対して、伝統工法の建物の場合は1/15 radian の層間変形角(傾斜角約4度)が破壊の目安となっています。
すなわち、伝統工法の建物は在来型の建物に比較して2倍の大きさの変形まで破壊の許容範囲が広いことを示しています。
以上のような考察から、伝統工法の建物の伝統耐震評価指数Ctを算定する場合には、伝統構法の建物の最大応答倍率Rtは、
R=Rt /2 と評価するのが妥当であることが分かります。
Ct=(T/Tt )2 √(Q Rt /2)
=25/√2 ・T2 ・√(Q ・Rt )
したがって、 Ct は √2/8 ・C に対応することになり、伝統構法の建物の伝統耐震性能評価指が算定されます。
在来型の小規模建物の伝統耐震性能の評価指数Cを建物の振動特性値、すなわち建物の固有周期T,共振性能を示すQ値 Q,および最大応答倍率Rの相乗積の大きさで表すことにするとき、同様な考え方で伝統工法の建物の伝統耐震診断の評価指数Ct を表す場合は、両者の基準固有周期と許容される最大応答倍率の相違点を考慮して Ct は、√2/8 ・C に対応することになることが分かります。